-
Bagaimana cara membuka akaun di FBS?
Klik butang 'Buka akaun' di laman web kami dan teruskan ke Laman Peribadi. Sebelum anda boleh mula berdagang, lengkapkan dahulu proses pengesahan profil anda. Sahkan alamat emel dan nombor telefon anda, sahkan ID anda. Prosedur ini menjamin keselamatan dana dan identiti anda. Sebaik anda selesai dengan semua prosedur keselamatan ini, pergi ke platform perdagangan yang menjadi pilihan anda, dan mulakan berdagang.
-
Bagaimana cara untuk mula berdagang?
Jika anda berumur 18+, anda boleh sertai FBS dan mulakan kembara FX anda. Untuk berdagang, anda perlukan sebuah akaun perbrokeran dan ilmu yang mencukupi tentang tindak-tanduk aset di pasaran kewangan. Mulakan dengan mempelajari ilmu-ilmu asas menerusi bahan-bahan pengajian percuma kami dan buka akaun di FBS. Mungkin anda mahu mencuba suasana perdagangan dengan wang maya di akaun Demo terlebih dahulu. Apabila anda sudah bersedia, masuk ke pasaran sebenar dan berdagang untuk berjaya.
-
Cara-cara mengeluarkan wang yang anda raih di FBS?
Prosedurnya jelas dan mudah. Pergi ke laman Pengeluaran di laman web, atau bahagian Kewangan di Laman Peribadi FBS dan akses Pengeluaran. Anda boleh dapatkan wang yang anda raih menerusi sistem pembayaran yang sama yang anda gunakan untuk deposit-deposit anda. Sekiranya anda mendanai akaun anda menerusi pelbagai kaedah, keluarkan keuntungan anda menerusi kaedah-kaedah yang sama, berkadaran dengan nisbah amaun deposit-deposit anda.
Value at risk
Nilai berisiko (VaR)
Apakah Itu Nilai Berisiko (VaR)?
Nilai berisiko (VaR) ialah statistik yang menunjukkan potensi kerugian kewangan dalam firma, portfolio atau posisi sepanjang tempoh tertentu. Metrik ini biasanya digunakan oleh bank-bank pelaburan dan perdagangan untuk penilaian risiko kewangan.
Memahami Nilai Berisiko (VaR)
Pemodelan VaR mengukur jumlah potensi kerugian, kebarangkalian ia terjadi, dan jangka masanya.
Menggunakan penilaian VaR dapat membantu menentukan risiko kumulatif daripada posisi yang dipegang oleh organisasi. Dengan menggunakan data yang diberikan oleh pemodelan VaR, institusi kewangan boleh memutuskan sama ada mereka mempunyai rizab modal yang mencukupi atau tidak untuk menampung kerugian. Mereka juga boleh memutuskan adakah risiko yang lebih tinggi daripada apa yang mereka boleh terima memerlukan mereka untuk membuat perubahan dalam portfolio mereka seterusnya memilih pelaburan dengan risiko yang lebih rendah.
Marginal Value at Risk (MVaR)
Nilai Berisiko Marginal atau Marginal Value at Risk (MVaR) ialah jumlah risiko tambahan yang dibawa oleh pelaburan baharu dalam portfolio. MVaR membantu pengurus untuk memahami perubahan risiko dalam portfolio akibat pengurangan atau penambahan pelaburan tertentu.
Suatu pelaburan mungkin mempunyai Nilai Berisiko yang tinggi. Walau bagaimanapun, jika ia berkorelasi secara negatif dengan portfolio, ia mungkin menyumbang jumlah risiko yang lebih rendah kepada portfolio berbanding risiko kendirinya.
Bagaimana Nilai Berisiko dikira
Terdapat tiga cara utama untuk mengira VaR: kaedah historikal, kaedah parametrik, dan kaedah Simulasi Monte Carlo. Setiap satunya berbeza dari segi pengiraan, kelebihan dan keburukan yang berkait dengan kerumitan, kelajuan pengiraan, kebolehgunaan pada instrumen kewangan tertentu dan faktor-faktor lain.
1. Kaedah historikal
Kaedah historikal adalah kaedah yang paling mudah untuk mengira Nilai Berisiko. Data pasaran untuk 100 hari terakhir diambil untuk mengira peratusan perubahan bagi setiap faktor risiko pada setiap hari. Setiap perubahan peratusan kemudiannya dikira dengan nilai pasaran semasa untuk mengunjurkan 100 senario untuk nilai masa hadapan.
Untuk setiap senario, portfolio dinilai menggunakan model harga bukan linear penuh. Hari terburuk kelima yang dipilih diandaikan berada pada 95% VaR.
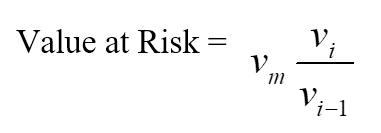
Di mana:
- vi ialah bilangan pembolehubah pada hari i,
- m ialah bilangan hari, dari mana data historikal diambil.
2. Kaedah parametrik
Kaedah parametrik juga dikenali sebagai kaedah varians-kovarians. Kaedah ini mengandaikan taburan normal sebagai pulangan. Dua faktor dianggarkan: pulangan yang dijangka dan sisihan piawai.
Kaedah parametrik adalah kaedah yang paling sesuai digunakan bagi masalah pengukuran risiko di mana taburannya diketahui dan dapat dianggarkan dengan andal. Kaedah ini menjadi tidak tepat apabila saiz sampel sangat kecil.
Kerugian ialah ‘l’ untuk portfolio ‘p’ yang mempunyai bilangan instrumen sebanyak ‘n’.
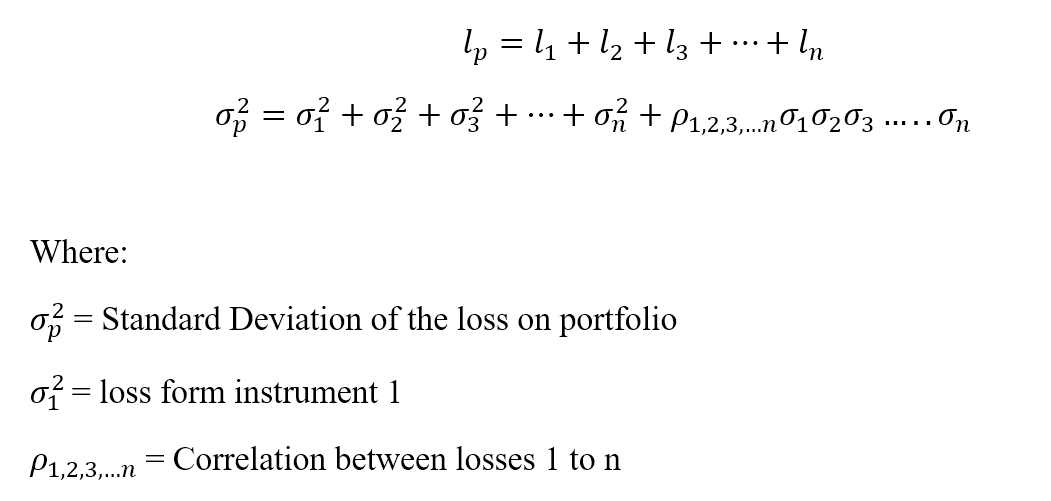
3. Kaedah Monte Carlo
Menurut kaedah Monte Carlo, Nilai Berisiko dikira dengan mencipta senario secara rawak bagi kadar masa hadapan menggunakan model penentuan harga bukan linear untuk menganggarkan perubahan nilai bagi setiap senario, kemudian VaR dikira berdasarkan kerugian yang paling teruk.
Kaedah Monte Carlo sesuai untuk kebanyakkan masalah pengukuran risiko, terutamanya apabila berhadapan dengan faktor-faktor yang rumit. Ia mengandaikan bahawa terdapat peruntukan kebarangkalian yang diketahui untuk faktor-faktor risiko.
Contoh VaR
Katakan pengurus risiko ingin mengira VaR 95% 1 hari untuk saham XYZ menggunakan data 100 hari. Menggunakan kaedah historikal, pengurus risiko akan melihat pulangan 100 hari terakhir untuk saham XYZ mengikut urutan daripada yang paling teruk kepada yang paling baik. Jika kita mempunyai 100 pulangan berikut, diisih dari yang terendah ke tertinggi:
VaR persentil ke-95, dalam kes ini, adalah bernilai -3.64% atau pengurus risiko boleh mengatakan bahawa VaR 95% sehari ialah kerugian sebanyak 3.64%. Jika jumlah risiko ini berada dalam julat yang boleh diterima oleh pengurus risiko, maka saham XYZ boleh dianggap sebagai pelaburan yang baik.
Kelebihan Nilai Berisiko (VaR)
1. Mudah untuk difahami
Nilai Berisiko ialah nombor yang menunjukkan tahap risiko portfolio. Nilai Berisiko diukur sama ada dalam unit harga atau sebagai peratusan, menjadikan tafsiran dan pemahaman VaR sangat mudah.
2. Kebolehgunaan
Nilai Berisiko boleh diaplikasikan kepada semua jenis aset: bon, saham, derivatif, mata wang, dsb. Oleh itu, institusi kewangan yang berbeza boleh menggunakan VaR untuk menilai keuntungan dan risiko pelaburan yang berlainan.
3. Universal
Nilai Berisiko digunakan secara meluas, menjadikannya sebagai standard yang diterima dalam urus niaga membeli, menjual atau pengesyoran aset.
Keterbatasan Nilai Berisiko
1. Portfolio besar
Mengira Nilai Berisiko untuk portfolio memerlukan pengiraan risiko dan pulangan bagi setiap aset dan hubung kait antara mereka. Jadi, semakin besar bilangan atau kepelbagaian aset dalam portfolio, semakin sukar untuk mengira VaR.
2. Perbezaan kaedah
Kaedah yang berbeza untuk mengira VaR boleh membawa kepada hasil yang berbeza bagi portfolio yang sama.
3. Andaian
Pengiraan VaR memerlukan beberapa andaian dibuat dan menggunakannya sebagai input. Jika andaian tidak betul, maka VaR juga akan menjadi salah.
Kesimpulan
Pengurusan portfolio sesebuah syarikat adalah proses yang kompleks yang memerlukan peningkatan kemahiran yang berterusan. Untuk perdagangan yang berjaya dalam pasaran Forex, seseorang pedagang harus mengikut peraturan pengurusan risiko, seperti saiz kedudukan, kepelbagaian dan mengehadkan kerugian dengan meletakkan pesanan Henti Kerugian, berdagang dengan leveraj, dan lain-lain. Mujurlah, FBS menawarkan pelbagai jenis bahan pembelajaran yang boleh membantu pedagang di mana-mana peringkat, dari pedagang baharu hingga berpengalaman, untuk meningkatkan keberhasilan perdagangan mereka.
2023-05-08 • Dikemaskini
